Rupi Adhikary
AP Calculus AB/BC ♾️
279 resourcesSee Units
What is a limit?
A limit denotes the behavior of a function as it approaches a certain value which is especially important in calculus. In mathematical terms, the limit is asking the question "What value is 'y' getting close to as 'x' approaches a number?" and its represented by the expression:
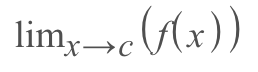
Out loud, this would sound something like "the limit of f(x) as x approaches c"
- The 'lim' shows that we're finding the limit and not the value of the function
- The 'x →c' tells us the value that x is getting closer and closer to but never actually reaching
- The 'f(x)' is meant to represent the functions you're working with
Three Criteria for Limits to Exist
1.) The limit of the function approaching from the right exists
- Graphically, this would look like following a function to a certain point on the x-axis from the right
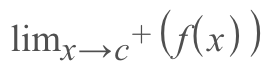
2.) The limit of the function approaching from the left exists
- Graphically, this would look like following a function to a certain point on the x-axis from the left
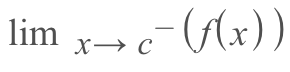
3.) The limit from the right equals the limit from the left
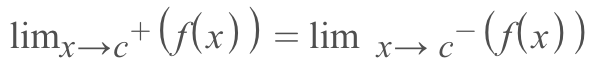
When doesn't a limit exist?
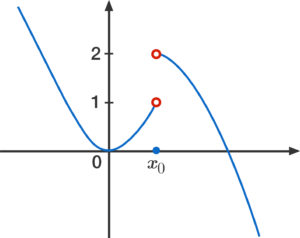
A limit MUST meet all three criteria in order for it to exist, which is important to remember especially when FRQ's come into play. If the limit from the left and the limit from the right are not equal, then the limit does not exist. An example of this would look something like this graph:
Here we can see that as we follow the function from the right hand side, it's going towards y = 2. On the left hand side, we see that the function is approaching y = 1. Since 2 ≄ 1, the limit does not exist at x = 1.
Limits Approaching Infinity
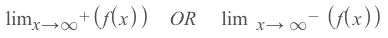
1.) Top-heavy
This is when the degree of the polynomial on the top of the function is greater than the degree of the polynomial in the denominator In this case, the answer you are finding is all dependent on whether or not you're being asked to be approaching negative or positive infinity. If you're approaching positive infinity, then the limit of a top-heavy function will also be infinity and vice versa.
2.) Middle-heavy
This is when the degrees of the numerator and denominator are the same. To find the limit here, you'll need to divide the leading coefficients of the numerator and denominator by each other.
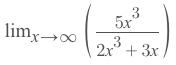
For example, here we see that the degrees of the top and bottom are 3 and that the leading coefficient of the numerator is 5 and 2 for the denominator. Therefore, the limit of f(x) as x approaches positive infinity is 5/2.
3.) Bottom-heavy
This is when the degree of the denominator is greater than that of the numerator. If a function is bottom heavy, then the limit is zero, regardless if it is approaching positive or negative infinity
📌Here are some extra resources to help you out on limits approaching infinity!
- https://www.mathwarehouse.com/calculus/limits/what-is-a-limit.php
- https://unit8limits.weebly.com/infinite-limits.html
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.