3.12 Quantum Mechanics and the Photoelectric Effect
4 min read•august 6, 2020
Kanya Shah
AP Chemistry 🧪
269 resourcesSee Units
Quantum Mechanics: Where is the Electron?
In the early days of chemistry, there were models of the atom all over the place. ⚛️
The first true model of an "atom" was the Dalton Model, which represented atoms as small balls bouncing off of each other. Of course, as you've probably learned, atoms aren't quite so simple.
The next model came with Thomson's Plum Pudding Model🍮 in the early 20th century, shortly after J.J. Thompson discovered the electron. This model represented the atom as a sea of positive charge with specks of negative charge - the electrons.
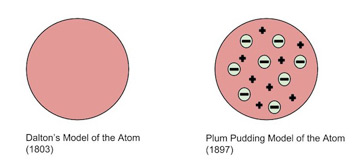
Image Courtesy of Study
From this point on, scientists knew two things about the model of the atom: there's a positive part and a negative part.
Shortly thereafter, Rutherford's gold foil💛 experiment showed that most of the atom was empty space.
👉While you don't need to necessarily know all of this history and all of these models for the AP Exam, understanding the foundations of chemistry help to build a foundation for the fundamental question for all of these models, and the question that created the field of quantum mechanics: where the heck do the electrons go?
While we won't exactly answer that exact question in this unit, it will be answered in part when you learn about electron orbitals.
Max Planck and the Ultraviolet Catastrophe
To understand where the electrons are in an atom, we must first understand how light and energy work together to form the basis for the quantum world. As we learned in the last lesson, light💡 can be represented as a wave of electromagnetic radiation permeating space.
One of the most important observations made was that when a piece of metal, or any body for that matter, was heated up enough, it released light. This makes sense! If you think about someone like a blacksmith, they take glowing hot metal and pound it into shape.
When discussing why exactly this happens, scientists hypothesized about a body that absorbed all light, known as a blackbody, which only absorbed and emitted light, but did not reflect any. However, when discussing light being radiated from a blackbody, it became clear that with this model, a body emits infinite amounts of light and thus infinite amounts of energy, creating the ultraviolet catastrophe. This theory broke laws of conservation of energy and frankly logic. When you put toast🍞 in a toaster, it does not burn your toast to smithereens, despite, according to the classical model, a blackbody should emit infinite energy.

The Ultraviolet Catastrophe. Image Courtesy of MSE 5317
Max Planck to the Rescue!
However, shortly after this catastrophe, a physicist named Max Planck solved the puzzle🧩. He theorized that light is emitted in discrete quantities - quanta (hence, quantum mechanics), which energy proportional to the frequency of the wave.
This can be represented in the equation E = hv, where E is the energy, v is the frequency and h is Planck's constant.
h = Planck's constant = 6.626 * 10^-34 Js (Joule seconds) - on the reference table
This equation helped form the basis for the eventual creation of quantum mechanics.
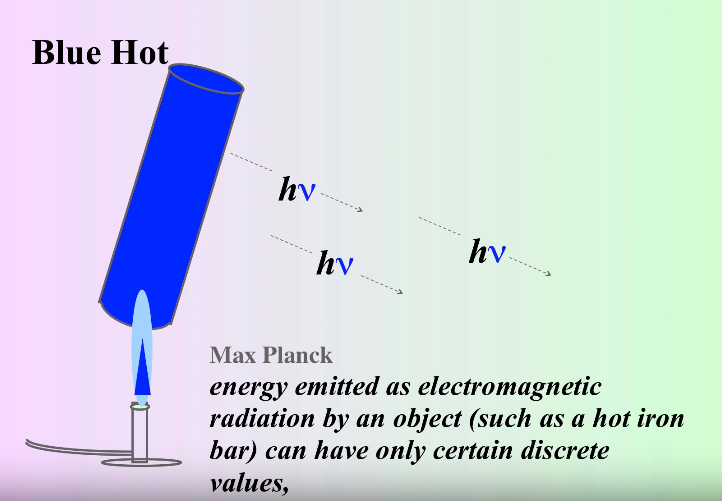
Quantized Light, Image Courtesy of MisterChemistry
The Photoelectric Effect
However, Planck's discovery was not immediately seen as revolutionary. It was not clear how amazing this discovery was until Albert Einstein uncovered the Photoelectric Effect, yet another mystery in physics.
Experiments showed that electrons were ejected from the surface of certain metals exposed to light of a minimum threshold frequency (and thus, as we've discussed, a minimum energy). Essentially, if you take a high enough frequency of light, you can zap⚡ electrons off of the surface of a metal, and this boggled the minds of physicists🤯. Einstein theorized that this was Planck's theory at work.
He theorized that light, in this case, was working like a particle - photons. Mathematically, this can be represented as saying that hv = KE of the electron + binding energy of the electron.
Because we know the hv is the energy of a wave of light (or now a photon), we know that if the energy of a photon exceeds the binding energy of an electron, the electron will be zapped away. Then, once we reach the threshold frequency, the kinetic energy of the photon increases as we lower the wavelength (or up the frequency, same thing) of the light.
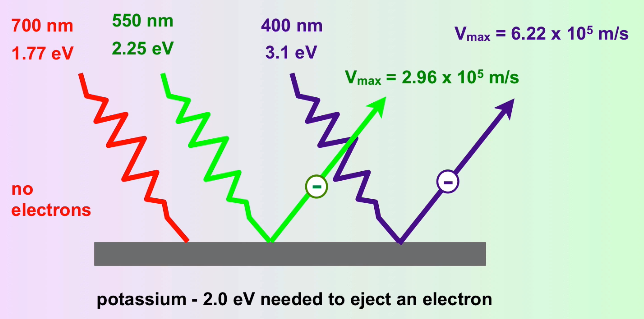
Image Courtesy of MisterChemistry
🎥Watch: AP Chemistry - The Photoelectric Effect
Speed of Light
There is one more equation to keep in mind besides E=hν and it relates the speed of light to both wavelength and frequency: c = λν
c = speed of light = 2.998 x 10^8 m/s
This equation is usually used in combination with the previous one. Together, they can help you solve an FRQ on the exam. Luckily, they are both listed on the AP Chemistry reference table🥳.
For an example, take a look at the FRQ we go over in 3.13!
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
✏️Frequently Asked Questions
✍️Free Response Questions
🧐Multiple Choice Questions
📆Big Reviews: Finals & Exam Prep

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.