2.7 Applications of Newton’s Second Law
3 min read•june 8, 2020
Peter Apps
AP Physics 1 🎡
257 resourcesSee Units
Essential Knowledge 4.A.1 ➰
The linear motion of a system can be described by the displacement, velocity, and acceleration of its center of mass. The variables x, v, and a all refer to the center-of-mass quantities.
If you recall from kinematics there are a few major equations that relate acceleration, displacement, initial and final velocity, and time together.

Variable Interpretation: Δx is horizontal displacement in meters, Vf is the final velocity in meters/second, Vo is initial velocity in meters/second, t is time in seconds, and a is acceleration in m/s/s.
⟶ In order to solve for a variable without having all four other quantities known, we look at the ‘Variable Missing’ column to pick the equation that best suits our question.
Essential Knowledge 4.A.2 🗯
The acceleration is equal to the rate of change of velocity with time, and velocity is equal to the rate of change of position with time.
Equation:
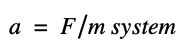
Equation:
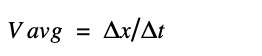
Equation:
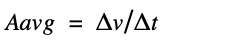
Essential Knowledge 4.A.3 🔊
Forces that the systems exert on each other are due to interactions between objects in the systems. If the interacting objects are parts of the same system, there will be no change in the center-of-mass velocity of that system.
Unfortunately, Newton’s Second Law also includes pretty infamous problems such as angular tension and apparent weight. Not to worry though, we’re going to break them down:
Key Concept: Angular Tension - mathematical problems when an object is held up by two or more strings at angles
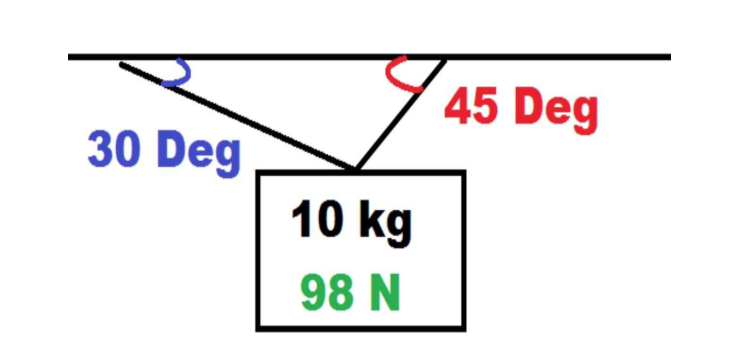
Image courtesy of VAM! Physics & Engineering.

🎥Watch: Organic Chemistry Tutor - Angular Tension
Key Concept: Apparent Weight - a property of objects that relates to how heavy an object is. The apparent weight of an object will be different from the true weight of an object when the Force of Gravity acting on that object is not balanced by an equal Normal Force.
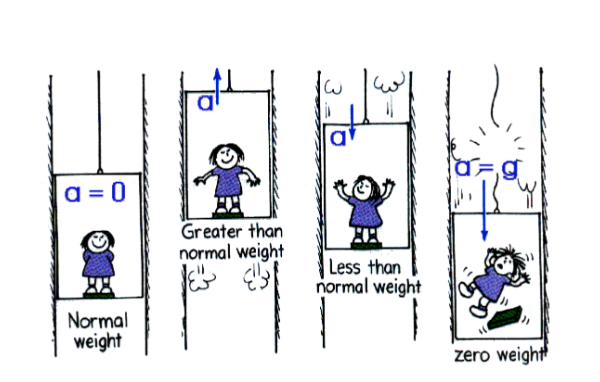
Image courtesy of physics.usask.ca
When you’re in an elevator going downwards and speeding up or going upwards and slowing down you tend to feel lighter. When you’re in an elevator going upwards and speeding up or going downwards and slowing down you tend to feel heavier. Why is that? To understand apparent weight fully, you must comprehend the four scenarios of the elevator problem:
When acceleration is upwards
The elevator accelerates upwards, but the inertia of a person would prefer to remain stationary, so the elevator floor must push up on the person with more force than their weight to accelerate them upwards. Therefore, Fn = ma + mg, so Normal Force is greater than true weight.
When acceleration is downwards
The elevator accelerates downwards, but the inertia of a person would prefer to remain stationary, so the elevator floor must drop out a little bit from underneath the person. This means the elevator floor must push up on the person less to support their weight, so Normal Force decreases. Therefore, Fn = mg - ma, so Normal Force is less than true weight.
When there is no acceleration
If the acceleration of an elevator is zero, the elevator is either moving with constant velocity or at rest. When this is the case Fn = mg, so Normal Force is equal to the true weight.
When an elevator is in free fall
If the elevator cable snaps, the elevator-person system will accelerate downwards at the rate of 9.8m/s/s (acceleration due to gravity). Since there is no contact between the floor of the elevator and the person Normal Force is zero. Therefore Normal Force is less than true weight.
🎥Watch: AP Physics 1 - Unit 2 Streams
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
👉AP Physics Essentials
🧐Multiple Choice Questions (MCQs)
✍️Free Response Questions (FRQs)
📆Big Reviews: Finals & Exam Prep

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.