Daniella Garcia-Loos
AP Physics C: Mechanics ⚙️
68 resourcesSee Units
4.1: Center of Mass 🏒
The center of mass, also sometimes called the center of gravity, is typically what we refer to as the geometric position in an object defined by: the mean position of every section of the object or system, weighted by mass. In other words, this is a place where the object is balanced in our gravitational field.
Below you can see an example of finding the center of mass in the x direction of a system of masses:

Image from LibreTexts
For a system of masses:
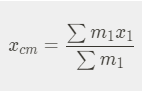
Calculus definition:
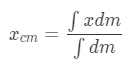
Another way to format the above formula is with linear mass density:
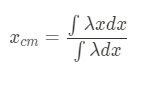
Linear mass density is typically a constant for something that is uniform, so it can be found with an equation like:
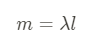
However, since AP loves to make us do calculus, we will sometimes see non-uniform objects! This means that the linear mass density would be a function.
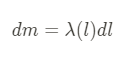
Let's try to calculate the center of mass of a uniform rod!
We can begin with one of the formulas we discussed above and place bounds on it:
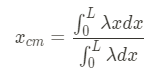
Since we know that the rod is uniform, we can take the linear mass density out of the integral because it is a constant.
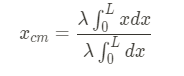
As you can see, the lambdas cancel out! Now we can evaluate the integrals.
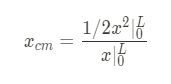
Now we can plug in our bounds and simplify. This leads us to:
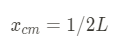
Hopefully, this answer seems intuitive to you! We'll be seeing problems similar to this when we tackle rotational inertia next unit.
Practice Questions
Even though AP Physics 1 is not calculus-based, we can practice applications of the center of mass with FRQs from that test too!
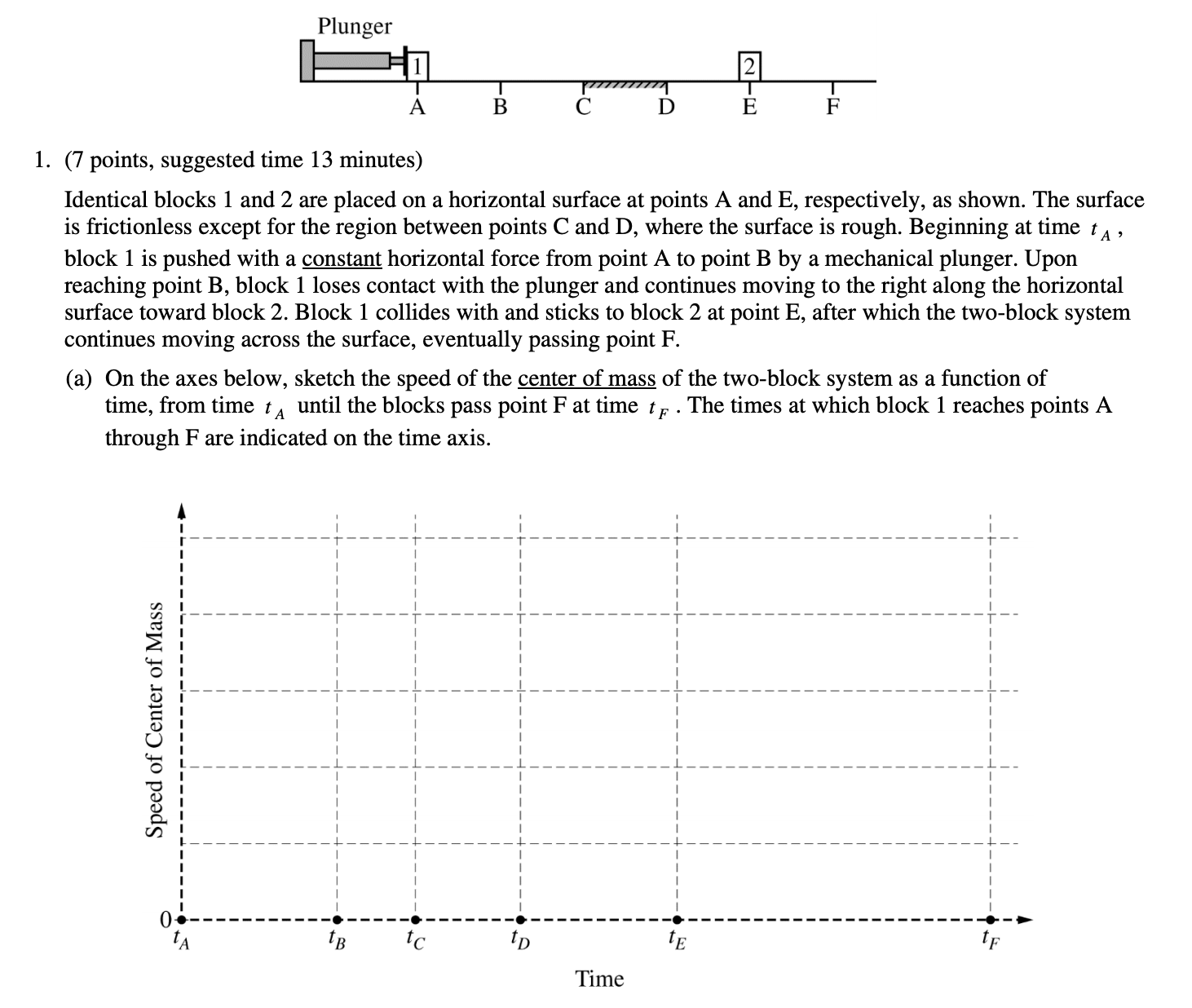
Taken from College Board
Answer:
The trick to this question is realizing that it is asking for the center of mass of the system. So the speed of it should only change when momentum isn't conserved, meaning when there is impulse!
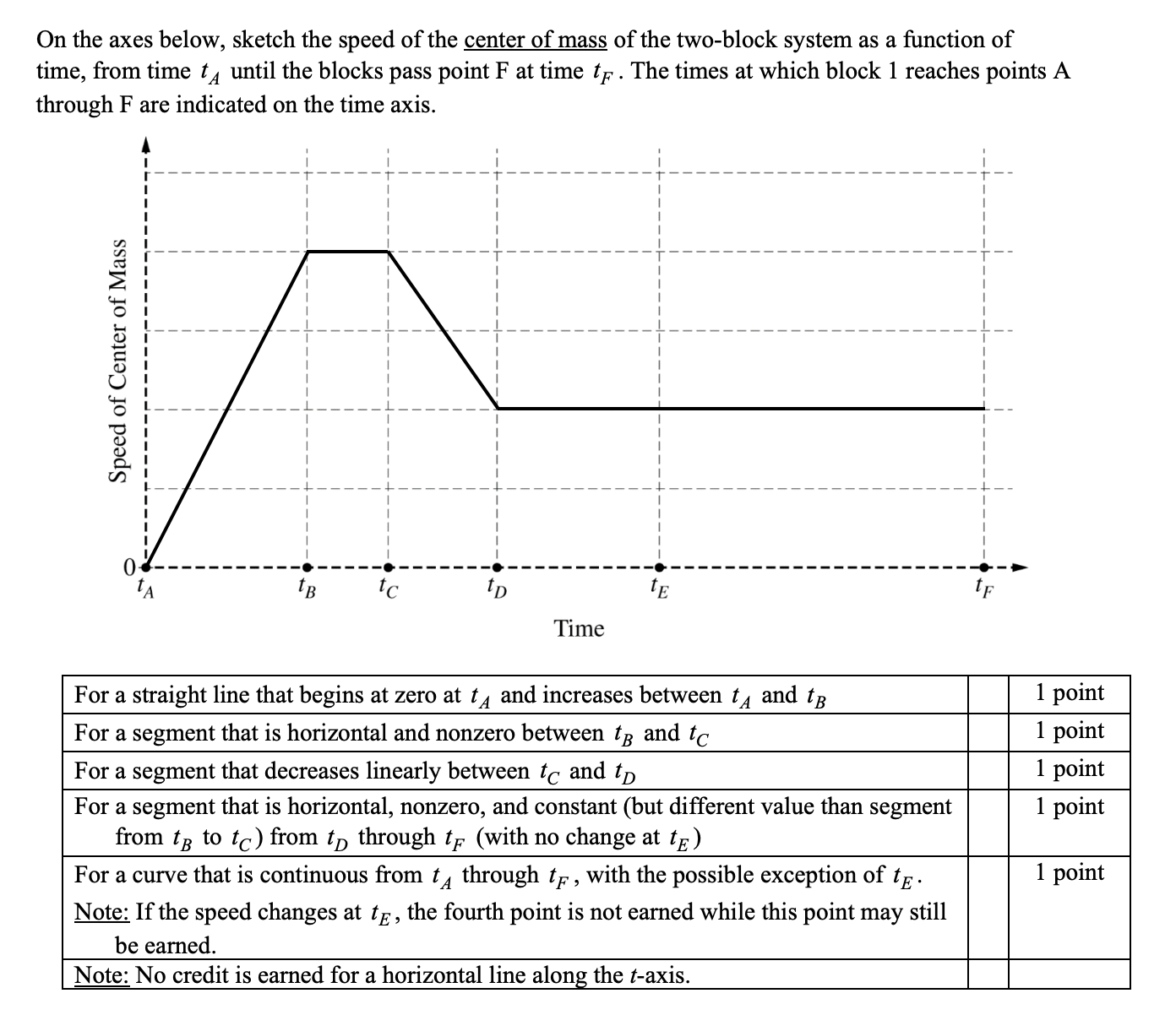
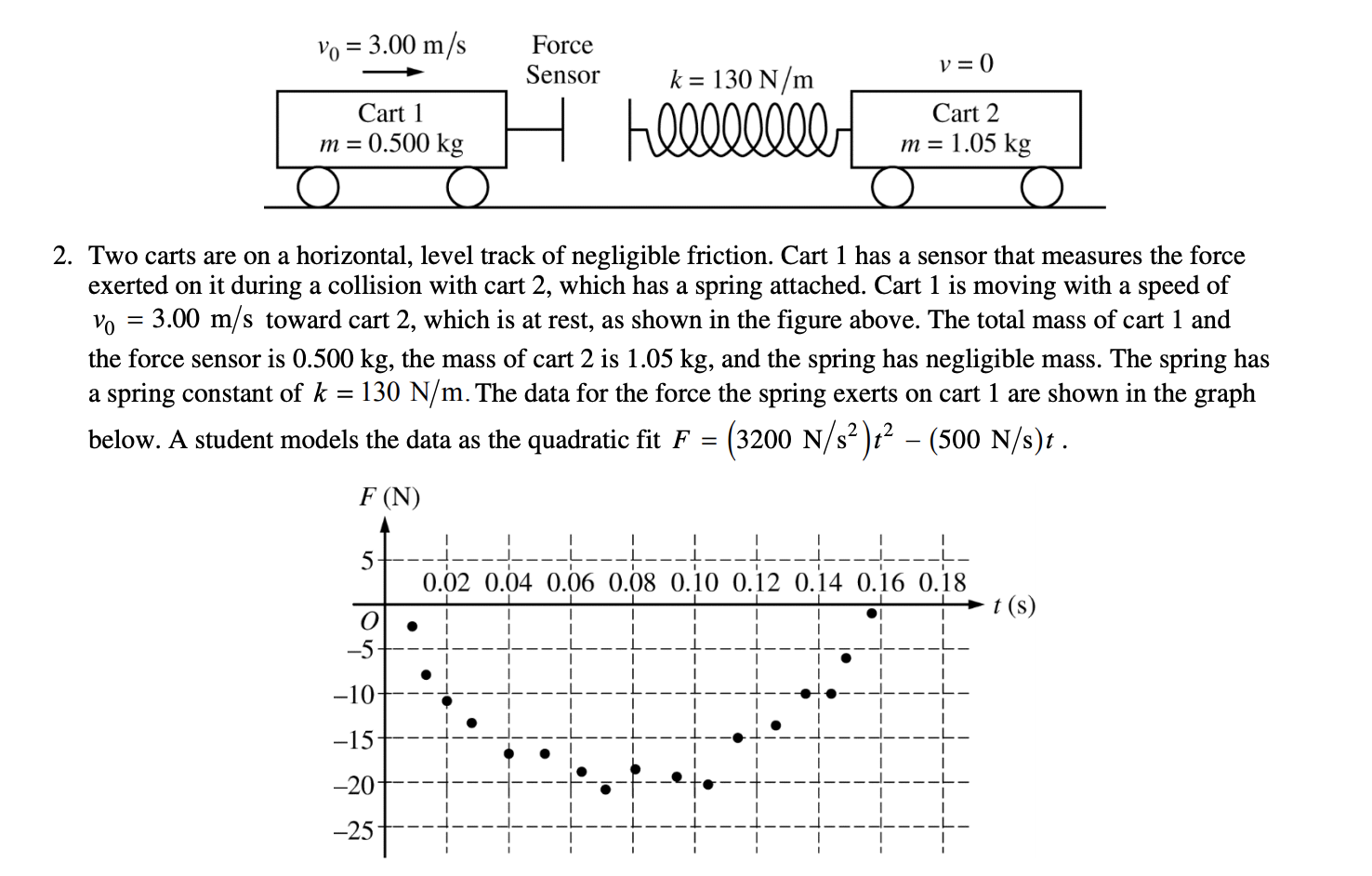
Answer:
Same focus as before, realize it is the center of mass of the system! Think of how you were searching for the x coordinate of the center of mass, you can apply the same strategy for velocity.

Browse Study Guides By Unit
🚗Unit 1 – Kinematics
🚀Unit 2 – Newton’s Laws of Motion
🎢Unit 3 – Work, Energy, & Power
🎳Unit 4 – Systems of Particles & Linear Momentum
🚲Unit 5 – Rotation
🌊Unit 6 – Oscillations
🪐Unit 7 – Gravitation
🙏Exam Reviews

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.