4.4 Biot–Savart Law and Ampère’s Law
4 min read•june 18, 2024
Peter Apps
AP Physics C: E&M 💡
26 resourcesSee Units
As promised in section 4.2, we're going to look at how we can define internal magnetic fields for wires of any configuration. There are two laws that help us to tackle this: Biot-Savart Law and Ampère’s Law.
Biot-Savart Law ☑️
The Biot-Savart Law lets us determine the magnetic field in a region of space that is caused by current in a wire. To solve this, we break up the wire into sections of length dl, each of which causes a small magnetic field dB.
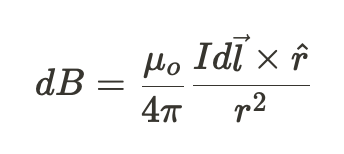
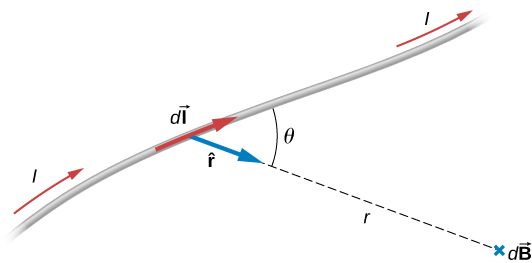
Image From phys.libretexts.org
\hat{r} is the unit vector and is equal to
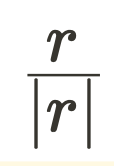
, and μ_o is the permeability of free space. This describes how well magnetic fields can propagate through space, similarly to how we used ε_0 to describe how well electric fields can propagate in Unit 1.
We often only care about the magnitude of the field, since we can usually find the direction of the field using the right-hand curl rule. Ignoring the directional aspect we find that:
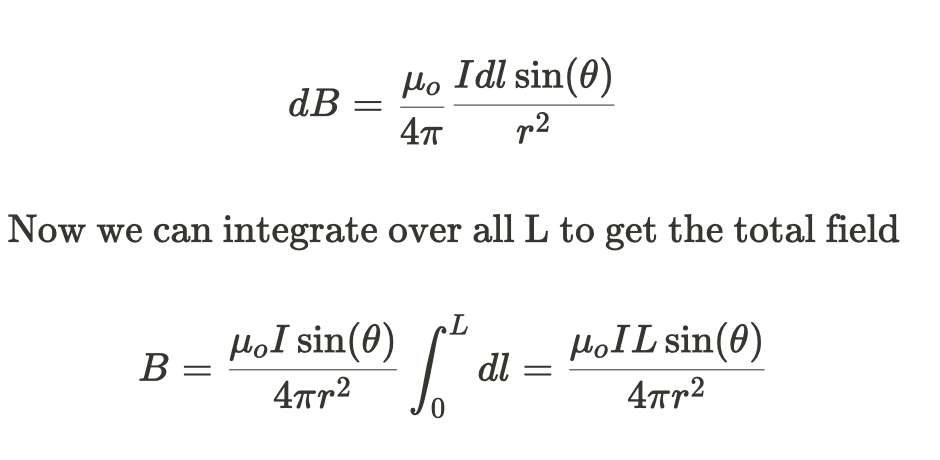
Common Geometries for using Biot-Savart Law 🧭
- Center of a Loop
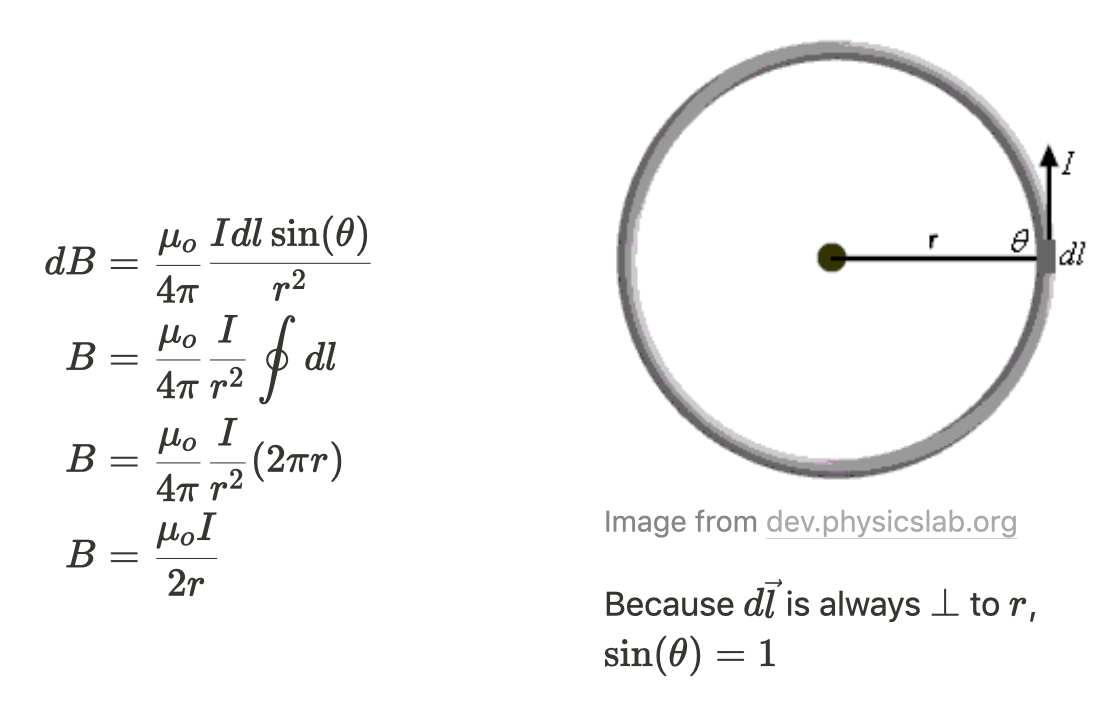
- On the axis of the center of a Loop
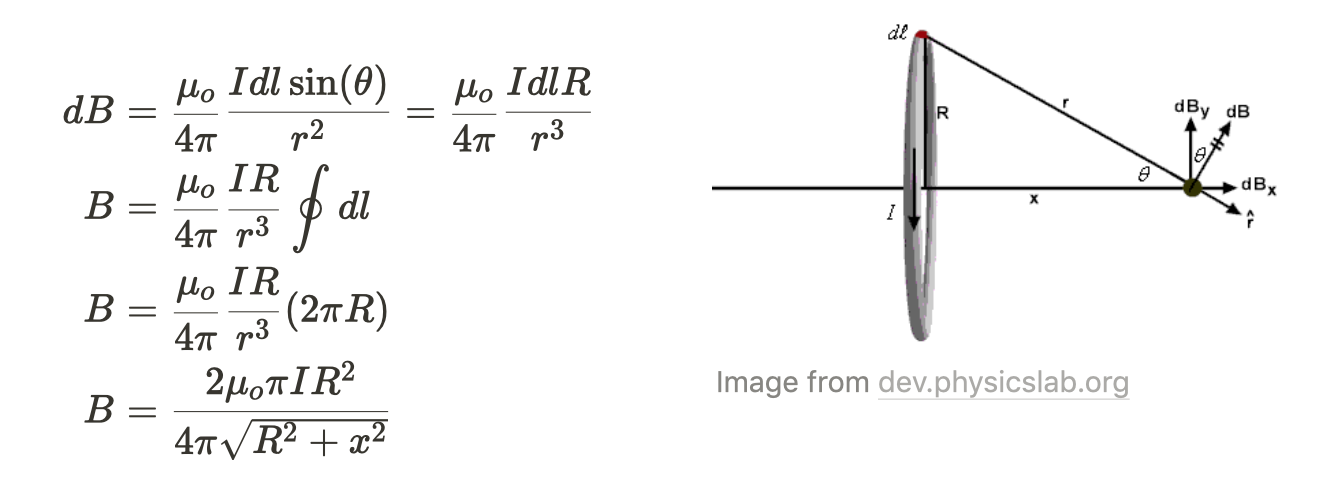
- Vertical components of the magnetic field cancel due to symmetry
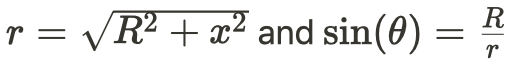
- (In)Finite Straight Wire
- Because the angle will change with respect to θ, we need to define r in terms of d and x

- If the wire is infinite in length, the integral becomes: (which is the equation we used in 4.2)
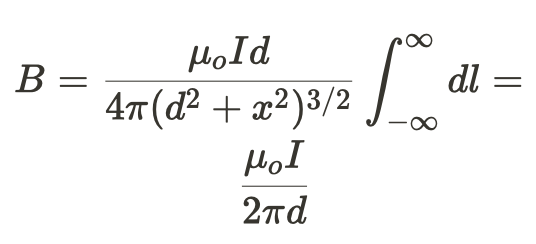
Ampère's Law ➰
Ampère's Law is the magnetic equivalent of Gauss' Law. This can be derived from the Biot-Savart law (if you're interested in how). We'll create a path around the object we care about, and then integrate to determine the enclosed current.
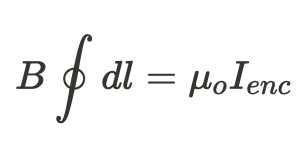
Let's use Ampere's Law to look at a pair of coaxial cables with currents running through both. We'll calculate the magnetic field at 4 different radii.
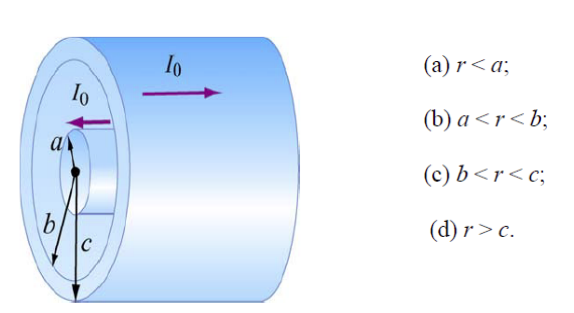
Image from web.iit.edu/
- r < a
- Some fraction of the current I_o is enclosed by our path.
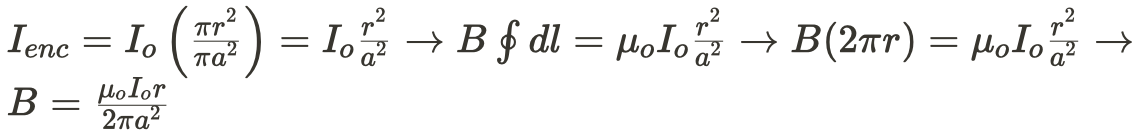
- a < r < b
- We now can enclose the entire current in the in inner cable.

- b < r < c
- We enclose all of the inner current, and need to subtract some portion of the outer current (since they're moving in different directions)

- r > c
- We encircle both cables, so I_enc = 0 and B = 0
Solenoids 🏎️
Solenoids create a special case where we need to apply Ampere's Law. A solenoid is basically a bunch of loops of wire tightly wound together. Its purpose is to produce a strong magnetic field as a current is passed through the wire. Every gas-powered car uses a solenoid to push a piston which starts the engine running. Without that 'starter' we'd be using hand cranks circa 1900.

Image from w
ikipedia.org
To apply Ampere's Law, we define our path as a rectangle enclosing a certain number of loops, N, in the solenoid. The current that is enclosed is equal to the current in the wire times N. If we add up the dl from the path, we'll get the total length of the solenoid. Your reference tables already use N as the # of charge carriers per volume, so we'll end up using n in our equation, where n = N/L.
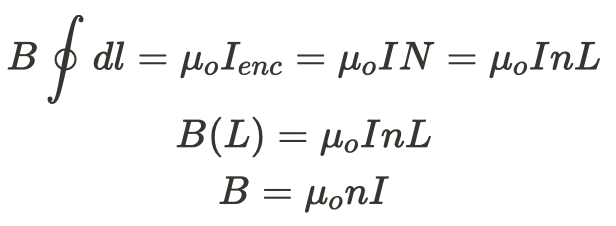
As you might have guessed, there's a right-hand rule for solenoids, too. Curl your fingers in the direction of the (conventional) current, and your thumb points in the direction of the magnetic field.
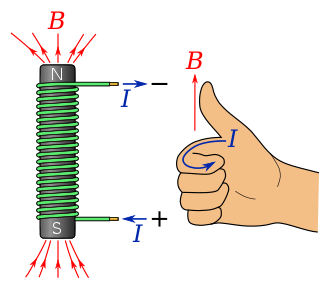
Image from wikipedia.org
Practice Questions
1)
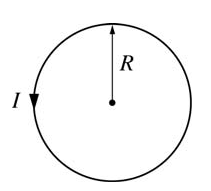
Image from apclassroom.collegeboard.org
The single, circular wire loop of radius R shown above carries a current I that produces a magnetic field B at the center of the loop. If the current remains constant while the loop is enlarged to a radius of 2R, what happens to the magnetic field at the center?
Answer
Using Biot-Savart Law

2)
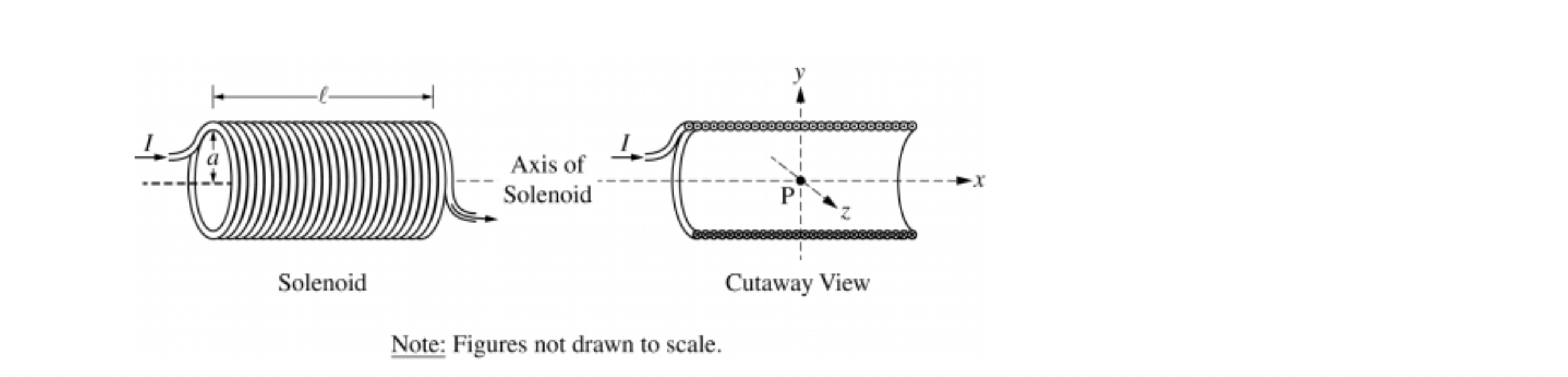
Image from collegeboard.org
A solenoid is used to generate a magnetic field. The solenoid has an inner radius a, length l, and N total turns of wire. A power supply, not shown, is connected to the solenoid and generates current I, as shown in the figure on the left above. The x-axis runs along the axis of the solenoid. Point P is in the middle of the solenoid at the origin of the xyz-coordinate system, as shown in the cutaway view on the right above. Assume l >> a.
(a) Select the correct direction of the magnetic field at point P. Justify your selection.
_ +x-direction, _ -x-direction, _ +y-direction, _ -y-direction, _ +z-direction, _ -z-direction
(b) i. On the cutaway view, clearly draw an Amperian loop that can be used to determine the magnetic field at point P at the center of the solenoid.
ii. Use Ampere's law to derive an expression for the magnetic field strength at point P. Express your answer in terms of I, l, N, a, and physical constants, as appropriate.
Answers
a) Use the Right Hand Rule to determine the direction of the induced current. (In this case for a solenoid, curve your fingers in the direction of the current.) Your fingers curl clockwise around the solenoid and your thumb points to the right (which is the positive x direction).
b)
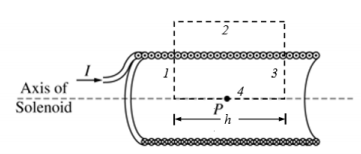
Image from collegeboard.org
ii. Similar to our derivation above. Remember n=N/l and because we're only getting part of the solenoid not the entire things, multiply by h not l to find the total enclosed current.
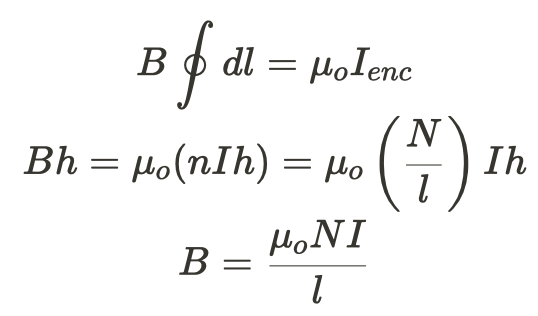
Browse Study Guides By Unit
⚡️Unit 1 – Electrostatics
🔋Unit 2 – Conductors, Capacitors, Dielectrics
🔌Unit 3 – Electric Circuits
🧲Unit 4 – Magnetic Fields
⚛️Unit 5 – Electromagnetism
📚Study Tools
📚Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.