Peter Apps
AP Physics 1 🎡
257 resourcesSee Units
Essential Knowledge 2.A.1 ⤵️
A vector field gives, as a function of position (and perhaps time), the value of a physical quantity that is described by a vector.
Key Concept: Vector Field - the assignment of a vector to each point in a portion of space. A vector field can be visualized as a collection of arrows with a given magnitude and direction, each attached to a point in the plane.

Image courtesy of Open University.
Uniform Circular Motion
As shown in the image above, a vector field can represent circular motion. From this vector field depiction, we can go into more depth of the specific components of uniform circular motion.
Key Concept: Uniform Circular Motion - the motion of an object in a circle at a constant speed that is accelerating due to a change in direction. In UCM there are four typical forces you will deal with: Tension, Friction, Gravity, and Normal. These forces are the cause of centripetal force.
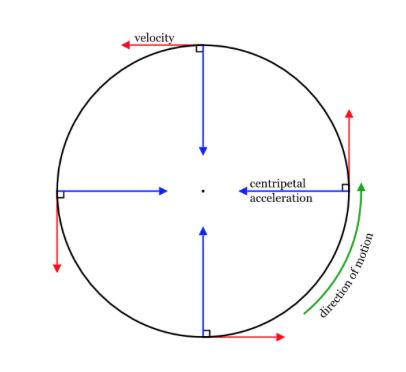
Image courtesy of Quizlet.
From this diagram, we can see in uniform circular motion centripetal acceleration is constant and always pointed towards the center, or center-seeking. Similarly, the centripetal force always points towards the center. However, velocity is tangent from the center; therefore, it is not considered in the net force. All forces pointing towards the center of the circle are positive (+) and all forces pointing away from the center of the circle are negative (-). Anything that doesn’t point away from or towards the circle’s center isn’t considered in the net force.
- Key Concept: Centrifugal - moving or tending to move away from a center.
- Key Concept: Centripetal - moving or tending to move toward a center.
- Key Concept: Centripetal Force - a force that acts on a body moving in a circular path and is directed toward the center around which the body is moving.
Equation: Fc = mv^2/r, where Fc is Centripetal Force in Newtons, m is mass in kilograms, v is the velocity in m/s, and r is the radius in meters.
A common misconception with centripetal force is that it is a new force when, in actuality, it is the net force inward and should be treated as such. To prove this concept, let’s dive into how the equation for centripetal force is derived: Newton’s second law gives us the equation F =ma, which can also be adapted for net force. Acceleration in a uniform circular motion is given as a = v^2/r, so Centripetal Force is simply mass x v^2/r or mv^2/r. Remember to not include centripetal force on any free-body diagrams because it is not a force, but rather the net force.
🎥Watch: AP Physics 1 - Unit 3 Streams
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
👉AP Physics Essentials
🧐Multiple Choice Questions (MCQs)
✍️Free Response Questions (FRQs)
📆Big Reviews: Finals & Exam Prep

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.