7.6 Finding General Solutions Using Separation of Variables

3 min read•june 18, 2024

AP Calculus AB/BC ♾️

279 resources

See Units

General Solutions

🎥 Watch: AP Calculus AB/BC - Separable Differential Equations

The separation of variables is a powerful method for solving differential equations and finding general solutions, which are defined as sets or families of functions that satisfy the conditions specified by the equation. This technique involves separating the variables on both sides of the equation, so that it can be solved for one variable at a time. The solution then takes the form of an explicit function that describes the behavior of the system being modeled.

While the concept of general solutions may seem abstract, it is based on the well-established principles of integration and antidifferentiation. The general solution provides a comprehensive and systematic approach to solving differential equations, as it includes all possible solutions that satisfy the conditions specified by the equation. 💯

This statement reads as “C is any real number, which implies f(x) + C is confined to a certain set of functions S.” Or, more simply put, this means that there are infinite solutions to Eq. 22, but the solution must include the condition that C is a constant that does not depend on x.

This means that f(x) + C is a general solution. A specific solution for this same example would be: C is a specific number. Differential equations function in a similar way. First, find a general solution, then find a specific solution if you are given more information. 📖

Recipe for Success

Here's another way to show the steps needed to solve a differential equation using separation of variables:

Write the differential equation in standard form, with the dependent variable on one side and the independent variable and its derivatives on the other side.
Separate the variables by writing the equation as the product of two functions, one that depends only on the dependent variable and one that depends only on the independent variable.
Integrate both sides of the equation with respect to their respective variables. This will result in a pair of separate integrals.
Solve the integrals, either analytically or using numerical methods.
Use the initial conditions to determine the constant of integration.
Combine the solution into a single function and simplify it if possible.
Check the solution to ensure that it satisfies the original differential equation and the initial conditions or boundary conditions.
Plot the solution, if desired, to visualize the behavior of the dependent variable.

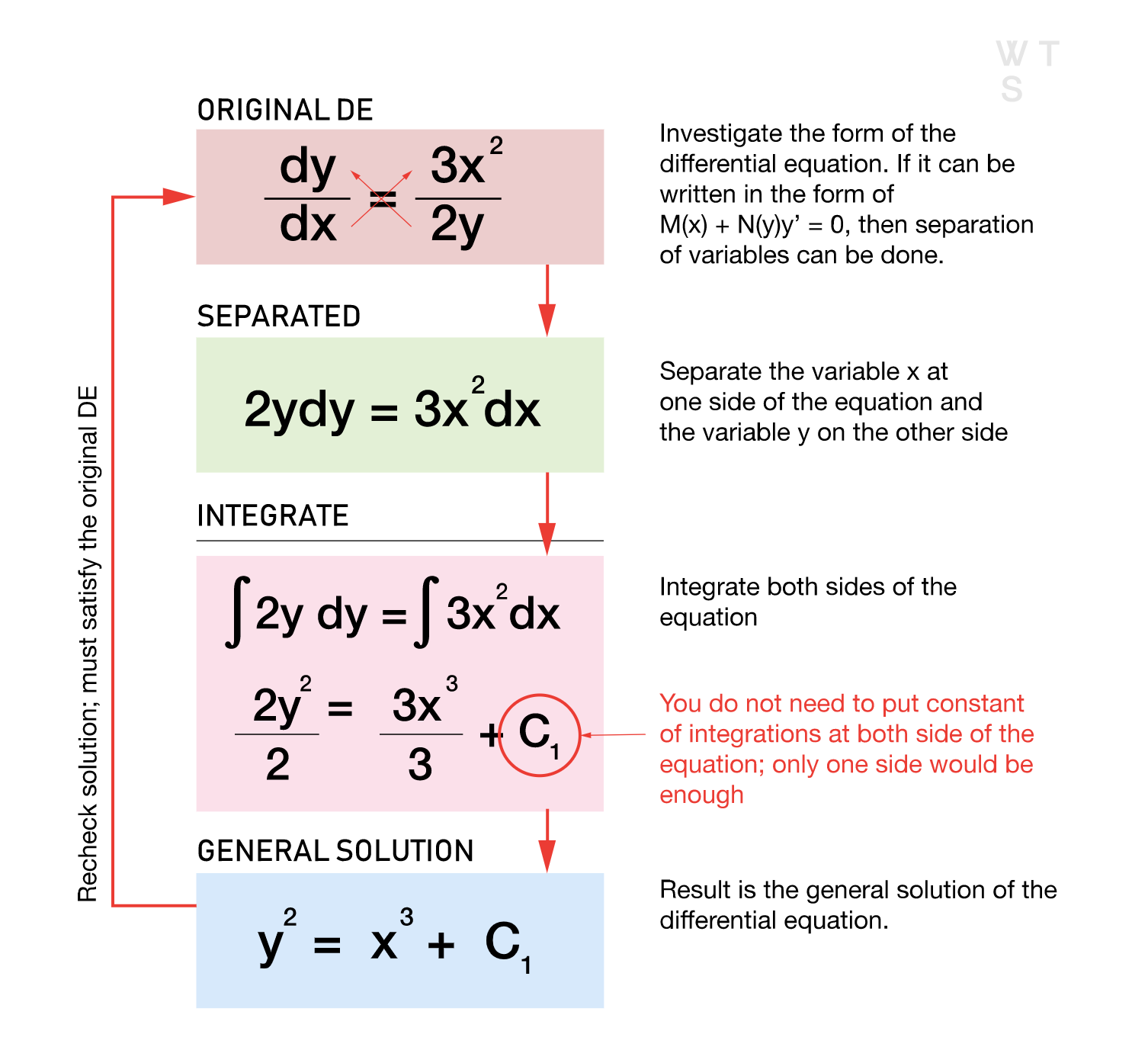
Source: WeTheStudy

Note that separation of variables may not always lead to a solution for a given differential equation, and other methods may need to be used instead. Additionally, the solution obtained using separation of variables may be an implicit solution, in which case further manipulation may be necessary to obtain an explicit solution. 🤔

To be continued in 7.7 Finding Particular Solutions Using Initial Conditions and Separation of Variables.

Browse Study Guides By Unit

👑Unit 1 – Limits & Continuity

🤓Unit 2 – Fundamentals of Differentiation

🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions

👀Unit 4 – Contextual Applications of Differentiation

✨Unit 5 – Analytical Applications of Differentiation

🔥Unit 6 – Integration & Accumulation of Change

💎Unit 7 – Differential Equations

7.0Exponential Models with Differential Equations

7.2Verifying Solutions for Differential Equations

7.3Sketching Slope Fields