7.2 Direction of Reversible Reactions

Like we discussed in the last section, equilibrium can be described as the settling of the rates of reversible reactions. These are reactions that can go forward (A → B) and backward (B → A) to form one full equilibrium reaction A ⇌ B. Equilibrium is the point at which the rates of these reactions equal, implying that the amount of A created is equal to the amount of B created over a period of time meaning that their concentrations do not change and the reaction mixture stays constant. We can represent this graphically by showing both the rates of reaction and the concentrations of the products and reactants as the reaction goes forward:

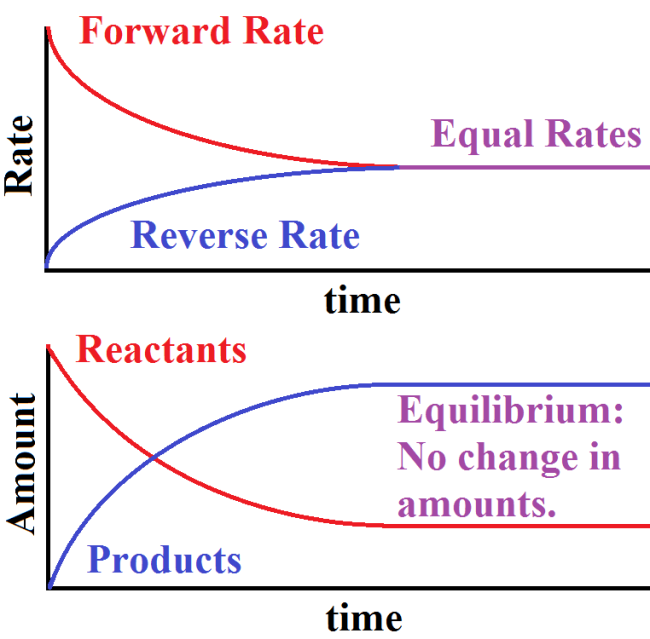
As we can see, when looking at a graph of rates, the forward reaction starts off as the reaction happening fastest but the reverse rate eventually catches up until the two are at equal rates. This can be seen further by looking at the amount of products and reactants present as the reaction goes forward. At first we see an accumulation of products because the forward rate exceeds the reverse rate implying a net creation of products. However, once equilibrium is reached, these values do not change. The reactions continue proceeding, just at equal rates.

When discussing equilibrium a topic that comes up a lot is whether a reaction is “product favored” or “reactant favored”. This concept describes whether a reaction goes forward more than backward or more backward rather than forward. In the picture above, we can see that this reaction is product favored because, at equilibrium, the concentration of products is larger than the concentrations of reactants. This can be represented mathematically as well by looking at values of K for a reaction.

If K < 1, the reaction is reactant favored (some K values can get into the range of 10^(-50)!)

If K > 1, the reaction is product favored (for some reactions K values are so large we say the reaction goes entirely forward)

If K = 1, we have an equal proportion of reactants and products at equilibrium. This is the least likely result.

Take a look at these examples of product favored and reactant favored reactions:

N2O4 ⇌ 2NO2 ⇒ K = 4.65 * 10^(-3). Because K < 1, this reaction is reactant favored

2O3 ⇌ 3O2 ⇒ K = 2.5 * 10^12. Because K > 1, this reaction is product favored

By observing whether a reaction is product favored or reactant favored we are able to draw some incredibly useful conclusions about how the reaction is going to proceed. It’s worth remembering that all reactions will produce some products and K tells us how much product is actually created. By observing K we can make qualitative judgements on how far forward a reaction goes. A higher K value implies that from reactants more products are created. For example, if we have two reactions and one has a K of 1.3*10^6 and the other 2.3*10^8, we know that both of these reactions are product favored but which one is more product favored? From observing the K values of each of these reactions we see that the second reaction will go farther forward than the first. In a similar vein we know that a reaction with a lower K value will not go as far forward. 

This way of thinking about K values proves incredibly useful especially when applying equilibrium to real life scenarios such as acids and bases. For example, consider acetic acid versus carbonic acid. For acetic acid, the reaction CH3COOH ⇌ CH3COO- + H+ has a K value of 1.8 * 10^(-5) whereas for carbonic acid the reaction H2CO3 ⇌ H+ + HCO3- has a K value of 4.3 * 10^(-7). From this information we can make a few useful conclusions. We see that carbonic acid’s dissociation has a lower K value meaning it will go further forward than acetic acid even though both are reactant favored. This tells us that with equal concentrations of acetic acid and carbonic acid, acetic acid will produce more H+ ions than H2CO3. From there we can evaluate that acetic acid is in fact a stronger acid than carbonic acid (at the same concentration). 

This section stands out as one of the most important conceptual sections of unit 7. In future units, the direction of a reversible reaction will be used to justify mathematical calculations and the ways that a reaction may react to external changes in pressure, concentration, and temperature. In fact, in the next section we’ll dive into one of these topics with our discussion of Q, the reaction quotient. By understanding this section in depth the mathematical calculations of unit 7 will be infinitely easier.